We've seen how data is represented as a sequence of values. What if we want to do something once for each value in the sequence? For instance, maybe we want to compute the sum of a sequence of numbers. How can we do that? The answer is to use iteration: in particular, we use a Python construct called a for-loop. Check it out:

OK, so that gives us a sequence of numbers (the sequence 5, 6, 11).

Notice how this works. We start out by setting total to hold the number 0. Then, we go through the sequence, one by one. For each number in the sequence, we temporarily set i to hold that number, and then we execute the statement total = total + i. This statement replaces the previous value of total with total + i. In other words, it adds i to the current running total. Once we've gone through the entire sequence, total holds the sum of all of the numbers in the sequence.

In short, a for-loop lets you do something once for each item in a sequence. It iterates through the sequence, examining each value one at a time, and does something for each.

In this case, we could have accomplished the same task without a for-loop: there is a numpy function we could have used (np.sum) to do this for us. That's not unusual; it's not unusual that there might be multiple ways to accomplish the same task. But sometimes there is no existing Python function that does exactly what we want, and that's when it is good to have tools we can use to do what we want.

Repetition¶

A special case of iteration is where we want to do some simple task multiple times: say, 10 times. You could copy-paste the code 10 times, but that gets a little tedious, and if you wanted to do it a thousand times (or a million times), forget it. Also, copy-pasting code is usually a bad idea: what if you realize you want to change some piece of it? Then you'll need to laboriously change each copy of it. Boooring!

A better solution is to use a for-loop for this purpose. The trick is to choose a sequence of length 10, and then iterate over the sequence: do the task once for each item in the sequence. It doesn't really matter what we put in the sequence; any sequence will do.

However, there is a standard idiom for what to put in the sequence. The typical solution is to create a sequence of consecutive integers, starting at 0, and iterate over it. If we wanted to do something 1000 times, we'd create a sequence holding the values 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Why 9? (and not 10?) Because that's where we need to end, if we want the list to have 10 items. (Why not use 1, 2, .., 10? I'm tempted to say, because computer scientists are just a tad odd. Actually, there are good reasons for this idiom, but don't worry about it right now.)

How do we create a sequence 0, 1, .., 9? It turns out we've already seen how to do that: use np.arange().

So, now I'm ready to show you how to do something 10 times:

Strings are sequences, too:

In this class, you're going to use this a lot for simulation. For instance, you might code up a way to simulate one round of some gambling game; then you can use a for-loop to repeat the simulation thousands of times and see how often we win. The great thing about computers is that they're incredibly good at doing a small task repeatedly many times, so this is a perfect match for what they're good at.

Randomized response¶

Next, we'll look at a technique that was designed several decades ago to help conduct surveys of sensitive subjects. Researchers wanted to ask participants a few questions: Have you ever had an affair? Do you secretly think you are gay? Have you ever shoplifted? Have you ever sung a Justin Bieber song in the shower? They figured that some people might not respond honestly, because of the social stigma associated with answering "yes". So, they came up with a clever way to estimate the fraction of the population who are in the "yes" camp, without violating anyone's privacy.

Here's the idea. We'll instruct the respondent to roll a fair 6-sided die, secretly, where no one else can see it. If the die comes up 1, 2, 3, or 4, then respondent is supposed to answer honestly. If it comes up 5 or 6, the respondent is supposed to answer the opposite of what their true answer would be. But, they shouldn't reveal what came up on their die.

Notice how clever this is. Even if the person says "yes", that doesn't necessarily mean their true answer is "yes" -- they might very well have just rolled a 5 or 6. So the responses to the survey don't reveal any one individual's true answer. Yet, in aggregate, the responses give enough information that we can get a pretty good estimate of the fraction of people whose true answer is "yes".

Let's try a simulation, so we can see how this works. We'll write some code to perform this operation. First, a function to simulate rolling one die:

Now we'll use this to write a function to simulate how someone is supposed to respond to the survey. The argument to the function is their true answer; the function returns what they're supposed to tell the interview.

We can try it. Assume our true answer is 'no'; let's see what happens this time:

Of course, if you were to run it again, you might get a different result next time.

OK, so this lets us simulate the behavior of one participant, using randomized response. Let's simulate what happens if we do this with 10,000 respondents. We're going to imagine asking 10,000 people whether they've ever sung a Justin Bieber song in teh shower. We'll imagine there are 10000 * p people whose true answer is "yes" and 10000 * (1-p) whose true answer is "no", so we'll use one for-loop to simulate the behavior each of the first 10000 * p people, and a second for-loop to simulate the behavior of the remaining 10000 * (1-p). We'll collect all the responses in a table, appending each response to the table as we receive it.

We get a giant table with 10,000 rows, one per simulated participant. Let's build a histogram and look at how many "yes"s we got and how many "no"s.

So we polled 10,000 people, and got back 3644 yes responses.

Exercise for you: Based on these results, approximately what fraction of the population has truly sung a Justin Bieber song in the shower?

Take a moment with your partner and work out the answer.

Summing up¶

This method is called "randomized response". It is one way to poll people about sensitive subjects, while still protecting their privacy. You can see how it is a nice example of randomness at work.

It turns out that randomized response has beautiful generalizations. For instance, your Chrome web browser uses it to anonymously report feedback to Google, in a way that won't violate your privacy. That's all we'll say about it for this semester, but if you take an upper-division course, maybe you'll get to see some generalizations of this beautiful technique.

The steps in the randomized response survey can be visualized using a tree diagram. The diagram partitions all the survey respondents according to their true and answer and the answer that they eventually give. It also displays the proportions of respondents whose true answers are 1 ("yes") and 0 ("no"), as well as the chances that determine the answers that they give. As in the code above, we have used p to denote the proportion whose true answer is 1.

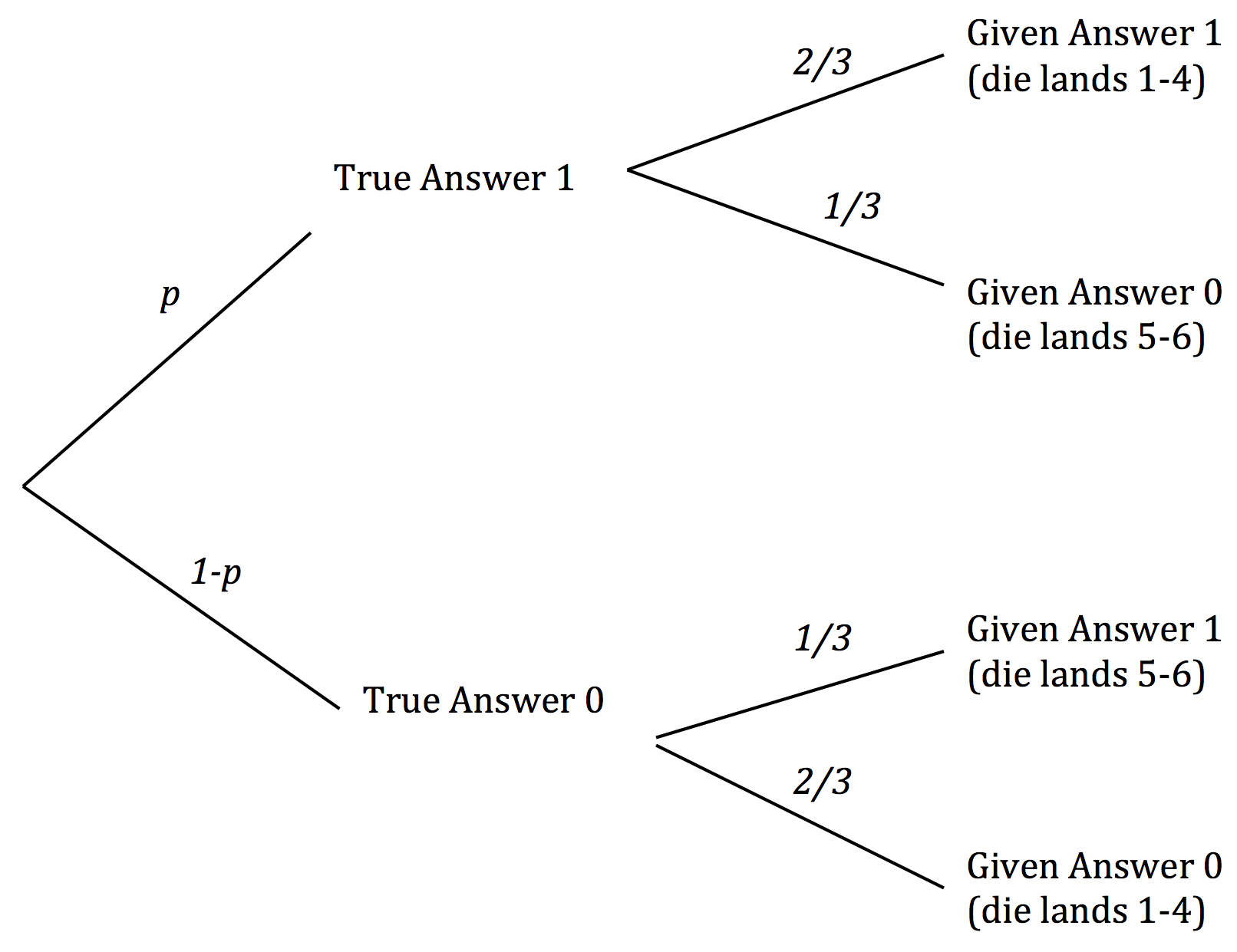
The respondents who answer 1 split into two groups. The first group consists of the respondents whose true answer and given answers are both 1. If the number of respondents is large, the proportion in this group is likely to be about 2/3 of p. The second group consists of the respondents whose true answer is 0 and given answer is 1. This proportion in this group is likely to be about 1/3 of 1-p.

We can observed $p^*$, the proportion of 1's among the given answers. Thus $$ p^* ~\approx ~ \frac{2}{3} \times p ~+~ \frac{1}{3} \times (1-p) $$

This allows us to solve for an approximate value of p: $$ p ~ \approx ~ 3p^* - 1 $$

In this way we can use the observed proportion of 1's to "work backwards" and get an estimate of p, the proportion in which whe are interested.

Technical note. It is worth noting the conditions under which this estimate is valid. The calculation of the proportions in the two groups whose given answer is 1 relies on each of the groups being large enough so that the Law of Averages allows us to make estimates about how their dice are going to land. This means that it is not only the total number of respondents that has to be large – the number of respondents whose true answer is 1 has to be large, as does the number whose true answer is 0. For this to happen, p must be neither close to 0 nor close to 1. If the characteristic of interest is either extremely rare or extremely common in the population, the method of randomized response described in this example might not work well.

Estimating the number of enemy aircraft¶

In World War II, data analysts working for the Allies were tasked with estimating the number of German warplanes. The data included the serial numbers of the German planes that had been observed by Allied forces. These serial numbers gave the data analysts a way to come up with an answer.

To create an estimate of the total number of warplanes, the data analysts had to make some assumptions about the serial numbers. Here are two such assumptions, greatly simplified to make our calculations easier.

1. There are N planes, numbered $1, 2, ... , N$.

2. The observed planes are drawn uniformly at random with replacement from the $N$ planes.

The goal is to estimate the number $N$.

Suppose you observe some planes and note down their serial numbers. How might you use the data to guess the value of $N$? A natural and straightforward method would be to simply use the largest serial number observed.

Let us see how well this method of estimation works. First, another simplification: Some historians now estimate that the German aircraft industry produced almost 100,000 warplanes of many different kinds, But here we will imagine just one kind. That makes Assumption 1 above easier to justify.

Suppose there are in fact $N = 300$ planes of this kind, and that you observe 30 of them. We can construct a table called serialno that contains the serial numbers 1 through $N$. We can then sample 30 times with replacement (see Assumption 2) to get our sample of serial numbers. Our estimate is the maximum of these 30 numbers.

As with all code involving random sampling, run it a few times to see the variation. You will observe that even with just 30 observations from among 300, the largest serial number is typically in the 250-300 range.

In principle, the largest serial number could be as small as 1, if you were unlucky enough to see Plane Number 1 all 30 times. And it could be as large as 300 if you observe Plane Number 300 at least once. But usually, it seems to be in the very high 200's. It appears that if you use the largest observed serial number as your estimate of the total, you will not be very far wrong.

Let us generate some data to see if we can confirm this. We will use iteration to repeat the sampling procedure numerous times, each time noting the largest serial number observed. These would be our estimates of $N$ from all the numerous samples. We will then draw a histogram of all these estimates, and examine by how much they differ from $N = 300$.

In the code below, we will run 750 repetitions of the following process: Sample 30 times at random with replacement from 1 through 300 and note the largest number observed.

To do this, we will use a for loop. As you have seen before, we will start by setting up an empty table that will eventually hold all the estimates that are generated. As each estimate is the largest number in its sample, we will call this table maxes.

For each integer (called i in the code) in the range 0 through 749 (750 total), the for loop executes the code in the body of the loop. In this example, it generates a random sample of 30 serial numbers, computes the maximum value, and augments the rows of maxes with that value.

Here is a histogram of the 750 estimates. First, notice that there is a bar to the right of 300. That is because intervals include the left end but not the right. The rightmost bar represents the samples for which the largest observed serial number was 300.

As you can see, the estimates are all crowded up near 300, even though in theory they could be much smaller. The histogram indicates that as an estimate of the total number of planes, the largest serial number might be too low by about 10 to 25. But it is extremely unlikely to be underestimate the true number of planes by more than about 50.

The empirical distribution of a statistic¶

In the example above, the largest serial number is called a statistic (singular!). A statistic is any number computed using the data in a sample.

The graph above is an empirical histogram. It displays the empirical or observed distribution of the statistic, based on 750 samples.

The statistic could have been different.

A fundamental consideration in using any statistic based on a random sample is that the sample could have come out differently, and therefore the statistic could have come out differently too.

Just how different could the statistic have been?

The empirical distribution of the statistic gives an idea of how different the statistic could be, because it is based on recomputing the statistic for each one of many random samples.

However, there might still be more samples that could be generated. If you generate all possible samples, and compute the statistic for each of them, then you will have a complete enumeration of all the possible values of the statistic and all their probabilities. The resulting distribution is called the probability distribution of the statistic, and its histogram is called the probability histogram.

The probability distribution of a statistic is also called the sampling distribution of the statistic, because it is based on all possible samples.

The probability distribution of a statistic contains more accurate information about the statistic than an empirical distribution does. So it is good to compute the probability distribution exactly when feasible. This becomes easier with some expertise in probability theory. In the case of the largest serial number in a random sample, we can calculate the probability distribution by methods used earlier in this class.

The probability distribution of the largest serial number¶

For ease of comparison with the proportions in the empirical histogram above, we will calculate the probability that the statistic falls in each of the following bins: 0 to 250, 250 to 260, 260 to 270, 270 to 280, 280 to 290, and 290 to 300. To be consistent with the binning convention of hist, we will work with intervals that include the left endpoint but not the right. Therefore we will also calculate the probability in the interval 300 to 310, noting that the only way the statistic can be in that interval is if it is exactly 300.

Let us start with the left-most interval. What is the chance that the largest serial number is less than 250? That is the chance that all the serial numbers are less than 250: $$ \left(\frac{249}{300}\right)^{30} ~ \approx ~ 0.00374 $$ We can express this quantity in terms of our population size N (300) and sample_size (30).

Similar reasoning gives us the chance that the largest serial number is in the interval 250 to 260, not including the right end. For this event to happen, the largest serial number must be less than 260 and not less than 250. In other words, all 30 serial numbers must be less than 290, and not all serial numbers must be less than 280. The chance of this is $$ \left(\frac{259}{300}\right)^{30} - \left(\frac{249}{300}\right)^{30} ~ \approx ~ 0.0084 $$

We can now gather these ideas into code that computes all of the probabilities. Like the leftmost interval, the rightmost interval gets its own calculation.

This histogram displays the exact probability distribution of the largest serial number in a sample of 30. For comparison, here again is the empirical distribution of the statistic based on 750 repetitions of the sampling process.

The two histograms are extremely similar. Because of the large number of repetitions of the sampling process, the empirical distribution of the statistic looks very much like the probability distribution of the statistic.

When an empirical distribution of a statistic is based on a large number of samples, then it is likely to be a good approximation to the probability distribution of the statistic. This is of great practical importance, because the probability distribution of a statistic can sometimes be complicated to calculate exactly.

Here is an example to illustrate this point. Thus far, we have used the largest observed serial number as an estimate of the total number of planes. But there are other possible estimates, and we will now consider one of them.

The idea underlying this estimate is that the average of the observed serial numbers is likely be about halfway between 1 and $N$. Thus, if $A$ is the average, then $$ A ~ \approx ~ \frac{1+N}{2} ~~~ \mbox{and so} ~~~ N \approx 2A - 1 $$

Thus a new statistic can be used to estimate the total number of planes: take the average of the observed serial numbers, double it, and subtract 1.

How does this method of estimation compare with using the largest number observed? For the new statistic, it turns out that calculating the exact probability distribution takes some effort. However, with the computing power that we have, it is easy to generate an empirical distribution based on repeated sampling.

So let us construct an empirical distribution of our new estimate, based on 750 repetitions of the sampling process. The number of repetitions is chosen to be the same as it was for the earlier estimate. This will allow us to compare the two empirical distributions.

Notice that unlike the earlier estimate, this one can overestimate the number of planes. This will happen when the average of the observed serial numbers is closer to $N$ than to 1.

Comparison of the two methods

To compare two histograms, we must use the same horizontal and vertical scales for both. Here are the empirical histograms of the new estimate and the old, both drawn to the same scale.

You can see that the old method almost always underestimates; formally, we say that it is biased. But it has low variability, and is highly likely to be close to the true total number of planes.

The new method overestimates about as often as it underestimates, and thus is called unbiased on average in the long run. However, it is more variable than the old estimate, and thus is prone to larger absolute errors.

This is an instance of a bias-variance tradeoff that is not uncommon among competing estimates. Which estimate you decide to use will depend on the kinds of errors that matter the most to you. In the case of enemy warplanes, underestimating the total number might have grim consequences, in which case you might choose to use the more variable method that overestimates about half the time. On the other hand, if overestimation leads to needlessly high costs of guarding against planes that don't exist, you might be satisfied with the method that underestimates by a modest amount.

By now we have seen many examples of situations in which one distribution appears to be quite close to another. The goal of this section is to quantify the difference between two distributions. This will allow our analyses to be based on more than the assessements that we are able to make by eye.

For this, we need a measure of the distance between two distributions. We will develop such a measure in the context of a study conducted in 2010 by the Americal Civil Liberties Union (ACLU) of Northern California.

The focus of the study was the racial composition of jury panels in Alameda County. A jury panel is a group of people chosen to be prospective jurors; the final trial jury is selected from among them. Jury panels can consist of a few dozen people or several thousand, depending on the trial. By law, a jury panel is supposed to be representative of the community in which the trial is taking place. Section 197 of California's Code of Civil Procedure says, "All persons selected for jury service shall be selected at random, from a source or sources inclusive of a representative cross section of the population of the area served by the court."

The final jury is selected from the panel by deliberate inclusion or exclusion: the law allows potential jurors to be excused for medical reasons; lawyers on both sides may strike a certain number of potential jurors from the list in what are called "peremptory challenges"; the trial judge might make a selection based on questionnaires filled out by the panel; and so on. But the initial panel is supposed to resemble a random sample of the population of eligible jurors.

The ACLU of Northern California compiled data on the racial composition of the jury panels in 11 felony trials in Alameda County in the years 2009 and 2010. In those panels, the total number of poeple who reported for jury service was 1453. The ACLU gathered demographic data on all of these prosepctive jurors, and compared those data with the composition of all eligible jurors in the county.

The data are tabulated below in a table called jury. For each race, the first value is the percentage of all eligible juror candidates of that race. The second value is the percentage of people of that race among those who appeared for the process of selection into the jury.

Some races are overrepresented and some are underrepresented on the jury panels in the study. A bar graph is helpful for visualizing the differences.

Total Variation Distance¶

To measure the difference between the two distributions, we will compute a quantity called the total variation distance between them. To compute the total variation distance, take the difference between the two proportions in each category, add up the absolute values of all the differences, and then divide the sum by 2.

Here are the differences and the absolute differences:

And here is the sum of the absolute differences, divided by 2:

The total variation distance between the distribution of eligible jurors and the distribution of the panels is 0.14. Before we examine the numercial value, let us examine the reasons behind the steps in the calculation.

It is quite natural to compute the difference between the proportions in each category. Now take a look at the column diff and notice that the sum of its entries is 0: the positive entries add up to 0.14, exactly canceling the total of the negative entries which is -0.14. The proportions in each of the two columns Panel and Eligible add up to 1, and so the give-and-take between their entries must add up to 0.

To avoid the cancellation, we drop the negative signs and then add all the entries. But this gives us two times the total of the positive entries (equivalently, two times the total of the negative entries, with the sign removed). So we divide the sum by 2.

We would have obtained the same result by just adding the positive differences. But our method of including all the absolute differences eliminates the need to keep track of which differences are positive and which are not.

Are the panels representative of the population?¶

We will now turn to the numerical value of the total variation distance between the eligible jurors and the panel. How can we interpret the distance of 0.14? To answer this, let us recall that the panels are supposed to be selected at random. It will therefore be informative to compare the value of 0.14 with the total variation distance between the eligible jurors and a randomly selected panel.

To do this, we will employ our skills at simulation. There were 1453 prosepective jurors in the panels in the study. So let us take a random sample of size 1453 from the population of eligible jurors.

[Technical note. Random samples of prospective jurors would be selected without replacement. However, when the size of a sample is small relative to the size of the population, sampling without replacement resembles sampling with replacement; the proportions in the population don't change much between draws. The population of eligible jurors in Alameda County is over a million, and compared to that, a sample size of about 1500 is quite small. We will therefore sample with replacement.]

The np.random.multinomial function draws a random sample uniformly with replacement from a population whose distribution is categorical. Specifically, np.random.multinomial takes as its input a sample size and an array consisting of the probabilities of choosing different categories. It returns the count of the number of times each category was chosen.

We can compare this distribution with the distribution of eligible jurors, by converting the counts to proportions. To do this, we will divide the counts by the sample size. It is clear from the results that the two distributions are quite similar.

As always, it helps to visualize:

The total variation distance between these distributions is quite small.

Comparing this to the distance of 0.14 for the panel quantifies our observation that the random sample is closer to the distribution of eligible jurors than the panel is.

However, the distance between the random sample and the eligible jurors depends on the sample; sampling again might give a different result.

How would random samples behave?

The total variation distance between the distribution of the random sample and the distribution of the eligible jurors is the statistic that we are using to measure the distance between the two distributions. By repeating the process of sampling, we can measure how much the statistic varies across different random samples. The code below computes the empirical distribution of the statistic based on a large number of replications of the sampling process.

Each row of the column above contains the total variation distance between a random sample and the population of eligible jurors.

The histogram of this column shows that drawing 1453 jurors at random from the pool of eligible candidates results in a distribution that rarely deviates from the eligible jurors' race distribution by more than 0.05.

How do the panels compare with random samples?

The panels in the study, however, were not quite so similar to the eligible population. The total variation distance between the panels and the population was 0.14, which is far out in the tail of the histogram above. It does not look like a typical distance between a random sample and the eligible population.

Our analysis supports the ACLU's conclusion that the panels were not representative of the population. The ACLU report discusses several reasons for the discrepancies. For example, some minority groups were underrepresented on the records of voter registration and of the Department of Motor Vehicles, the two main sources from which jurors are selected; at the time of the study, the county did not have an effective process for following up on prospective jurors who had been called but had failed to appear; and so on. Whatever the reasons, it seems clear that the composition of the jury panels was different from what we would have expected in a random sample.

A Classical Interlude: the Chi-Squared Statistic¶

"Do the data look like a random sample?" is a question that has been asked in many contexts for many years. In classical data analysis, the statistic most commonly used in answering this question is called the $\chi^2$ ("chi squared") statistic, and is calculated as follows:

Step 1. For each category, define the "expected count" as follows: $$ \mbox{expected count} ~=~ \mbox{sample size} \times \mbox{proportion in population} $$ This is the count that you would expect in that category, in a randomly chosen sample.

Step 2. For each category, compute $$ \frac{(\mbox{observed count - expected count})^2}{\mbox{expected count}} $$

Step 3. Add up all the numbers computed in Step 2.

A little algebra shows that this is equivalent to:

Alternative Method, Step 1. For each category, compute $$ \frac{(\mbox{sample proportion - population proportion})^2}{\mbox{population proportion}} $$

Alternative Method, Step 2. Add up all the numbers you computed in the step above, and multiply the sum by the sample size.

It makes sense that the statistic should be based on the difference between proportions in each category, just as the total variation distance is. The remaining steps of the method are not very easy to explain without getting deeper into mathematics.

The reason for choosing this statistic over any other was that statisticians were able to come up a formula for its approximate probability distribution when the sample size is large. The distribution has an impressive name: it is called the $\chi^2$ distribution with degrees of freedom equal to 4 (one fewer than the number of categories). Data analysts would compute the $\chi^2$ statistic for their sample, and then compare it with tabulated numerical values of the $\chi^2$ distributions.

Simulating the $\chi^2$ statistic.

The $\chi^2$ statistic is just a statistic like any other. We can use the computer to simulate its behavior even if we have not studied all the underlying mathematics.

For the panels in the ACLU study, the $\chi^2$ statistic is about 348:

To generate the empirical distribution of the statistic, all we need is a small modification of the code we used for simulating total variation distance:

Here is a histogram of the empirical distribution of the $\chi^2$ statistic. The simulated values of $\chi^2$ based on random samples are considerably smaller than the value of 348 that we got from the jury panels.

In fact, the long run average value of $\chi^2$ statistics is equal to the degrees of freedom. And indeed, the average of the simulated values of $\chi^2$ is close to 4, the degrees of freedom in this case.

In this situation, random samples are expected to produce a $\chi^2$ statistic of about 4. The panels, on the other hand, produced a $\chi^2$ statistic of 348. This is yet more confirmation of the conclusion that the panels do not resemble a random sample from the population of eligible jurors.

U.S. Supreme Court, 1965: Swain vs. Alabama¶

In the early 1960's, in Talladega County in Alabama, a black man called Robert Swain was convicted of raping a white woman and was sentenced to death. He appealed his sentence, citing among other factors the all-white jury. At the time, only men aged 21 or older were allowed to serve on juries in Talladega County. In the county, 26% of the eligible jurors were black, but there were only 8 black men among the 100 selected for the jury panel in Swain's trial. No black man was selected for the trial jury.

In 1965, the Supreme Court of the United States denied Swain's appeal. In its ruling, the Court wrote "... the overall percentage disparity has been small and reflects no studied attempt to include or exclude a specified number of Negroes."

Let us use the methods we have developed to examine the disparity between 8 out of 100 and 26 out of 100 black men in a panel drawn at random from among the eligible jurors.

As our test statistic, we will use the number of black men in a random sample of size 100. Here are the results of replicating the sampling procedure numerous times and counting the number of black men in each sample.

The numbers of black men in the first 10 repetitions were quite a bit larger than 8. The empirical histogram below shows the distribution of the test statistic over all the repetitions.

If the 100 men in Swain's jury panel had been chosen at random, it would have been extremely unlikely for the number of black men on the panel to be as small as 8. We must conclude that the percentage disparity was larger than the disparity expected due to chance variation.

Method and Terminology of Statistical Tests of Hypotheses¶

We have developed some of the fundamental concepts of statistical tests of hypotheses, in the context of examples about jury selection. Using statistical tests as a way of making decisions is standard in many fields and has a standard terminology. Here is the sequence of the steps in most statistical tests, along with some terminology and examples.

STEP 1: THE HYPOTHESES

All statistical tests attempt to choose between two views of how the data were generated. These two views are called hypotheses.

The null hypothesis. This says that the data were generated at random under clearly specified assumptions that make it possible to compute chances. The word "null" reinforces the idea that if the data look different from what the null hypothesis predicts, the difference is due to nothing but chance.

In both of our examples about jury selection, the null hypothesis is that the panels were selected at random from the population of eligible jurors. Though the racial composition of the panels was different from that of the populations of eligible jurors, there was no reason for the difference other than chance variation.

The alternative hypothesis. This says that some reason other than chance made the data differ from what was predicted by the null hypothesis. Informally, the alternative hypothesis says that the observed difference is "real."

In both of our examples about jury selection, the alternative hypothesis is that the panels were not selected at random. Something other than chance led to the differences between the racial composition of the panels and the racial composition of the populations of eligible jurors.

STEP 2: THE TEST STATISTIC

In order to decide between the two hypothesis, we must choose a statistic upon which we will base our decision. This is called the test statistic.

In the example about jury panels in Alameda County, the test statistic we used was the total variation distance between the racial distributions in the panels and in the population of eligible jurors. In the example about Swain versus the State of Alabama, the test statistic was the number of black men on the jury panel.

Calculating the observed value of the test statistic is often the first computational step in a statistical test. In the case of jury panels in Alameda County, the observed value of the total variation distance between the distributions in the panels and the population was 0.14. In the example about Swain, the number of black men on his jury panel was 8.

STEP 3: THE PROBABILITY DISTRIBUTION OF THE TEST STATISTIC, UNDER THE NULL HYPOTHESIS

This step sets aside the observed value of the test statistic, and instead focuses on what the value might be if the null hypothesis were true. Under the null hypothesis, the sample could have come out differently due to chance. So the test statistic could have come out differently. This step consists of figuring out all possible values of the test statistic and all their probabilities, under the null hypothesis of randomness.

In other words, in this step we calculate the probability distribution of the test statistic pretending that the null hypothesis is true. For many test statistics, this can be a daunting task both mathematically and computationally. Therefore, we approximate the probability distribution of the test statistic by the empirical distribution of the statistic based on a large number of repetitions of the sampling procedure.

This was the empirical distribution of the test statistic – the number of black men on the jury panel – in the example about Swain and the Supreme Court:

STEP 4. THE CONCLUSION OF THE TEST

The choice between the null and alternative hypotheses depends on the comparison between the results of Steps 2 and 3: the observed test statistic and its distribution as predicted by the null hypothesis.

If the two are consistent with each other, then the observed test statistic is in line with what the null hypothesis predicts. In other words, the test does not point towards the alternative hypothesis; the null hypothesis is better supported by the data.

But if the two are not consistent with each other, as is the case in both of our examples about jury panels, then the data do not support the null hypothesis. In both our examples we concluded that the jury panels were not selected at random. Something other than chance affected their composition.

How is "consistent" defined? Whether the observed test statistic is consistent with its predicted distribution under the null hypothesis is a matter of judgment. We recommend that you provide your judgment along with the value of the test statistic and a graph of its predicted distribution. That will allow your reader to make his or her own judgment about whether the two are consistent.

If you do not want to make your own judgment, there are conventions that you can follow. These conventions are based on what is called the observed significance level or P-value for short. The P-value is a chance computed using the probability distribution of the test statistic, and can be approximated by using the empirical distribution in Step 3.

Practical note on P-values and conventions. Place the observed test statistic on the horizontal axis of the histogram, and find the proportion in the tail starting at that point. That's the P-value.

If the P-value is small, the data support the alternative hypothesis. The conventions for what is "small":

• If the P-value is less than 5%, the result is called "statistically significant."

• If the P-value is even smaller – less than 1% – the result is called "highly statistically significant."

More formal definition of P-value. The P-value is the chance, under the null hypothesis, that the test statistic is equal to the value that was observed or is even further in the direction of the alternative.

The P-value is based on comparing the observed test statistic and what the null hypothesis predicts. A small P-value implies that under the null hypothesis, the value of the test statistic is unlikely to be near the one we observed. When a hypothesis and the data are not in accord, the hypothesis has to go. That is why we reject the null hypothesis if the P-value is small.

HISTORICAL NOTE ON THE CONVENTIONS

The determination of statistical significance, as defined above, has become standard in statistical analyses in all fields of application. When a convention is so universally followed, it is interesting to examine how it arose.

The method of statistical testing – choosing between hypotheses based on data in random samples – was developed by Sir Ronald Fisher in the early 20th century. Sir Ronald might have set the convention for statistical significance somewhat unwittingly, in the following statement in his 1925 book Statistical Methods for Research Workers. About the 5% level, he wrote, "It is convenient to take this point as a limit in judging whether a deviation is to be considered significant or not."

What was "convenient" for Sir Ronald became a cutoff that has acquired the status of a universal constant. No matter that Sir Ronald himself made the point that the value was his personal choice from among many: in an article in 1926, he wrote, "If one in twenty does not seem high enough odds, we may, if we prefer it draw the line at one in fifty (the 2 percent point), or one in a hundred (the 1 percent point). Personally, the author prefers to set a low standard of significance at the 5 percent point ..."

Fisher knew that "low" is a matter of judgment and has no unique definition. We suggest that you follow his excellent example. Provide your data, make your judgment, and explain why you made it.

Comparing Two Groups¶

The examples above investigate whether a sample appears to be chosen randomly from an underlying population. A similar line of reasoning can be used to determine whether two parts of a population are different. In particular, given two groups that differ in some distinguishing characteristic, we can investigate whether they are the same or different in another aspect.

Example: Married Couples and Umarried Partners¶

The methods that we have developed allow us to think inferentially about data from a variety of sources. Our next example is based on a study conducted in 2010 under the auspices of the National Center for Family and Marriage Research.

In the United States, the proportion of couples who live together but are not married has been rising in recent decades. The study involved a national random sample of over 1,000 heterosexual couples who were either married or living together but unmarried. One of the goals of the study was to compare the attitudes and experiences of the married and umarried couples.

The table below shows a subset of the data collected in the study. Each row corresponds to one person. The variables that we will examine in this section are:

• mar_status: 1=married, 2=unmarried
• empl_status: employment status; categories described below
• gender: 1=male, 2=female
• age: Age in years

We can improve the legibility of this table by converting numeric codes to text labels. The first two columns consist of the numerical codes assigned by the study to each person's marital status and employment status.

The describe function uses np.choose, a function that takes a sequences of indices and a sequence of labels. It returns a list that is the same length as the sequence of indices, but contains the label (from the sequence of labels) corresponding to each instance. It's useful for converting numeric codes into text.

Above, the first four columns are unchanged except for their labels. The next three columns interpret the codes for marital status, employment status, and gender. The final column is always 1, indicating that each row corresponds to 1 person.

Let us consider just the males first. There are 742 married couples and 292 unmarried couples, and all couples in this study had one male and one female, making 1,034 males in all.

Societal norms have changed over the decades, and there has been a gradual acceptance of couples living together without being married. Thus it is natural to expect that unmarried couples will in general consist of younger people than married couples. The histograms of the ages of the married and unmarried men show that this is indeed the case:

The difference is even more marked when we compare the married and unmarried women. The plots.ylim call ensures that all four histograms have been drawn to the same scale, for ease of comparison.

If married couples are in general older, they might differ from unmarried couples in other ways as well. For example, they might tend to be more wealthy or more educated than unmarried couples. Since both of those variables are associated with employment, the next variable that we will examine will be the employment status of the men.

Contingency Tables¶

The pivot method operates on a table in which each row is classified according to two variables (marital status and employment status, in this example). It returns what is known as a contingency table of the counts. A contingency table consists of a cell for each pair of categories that can be formed by taking one category of the first variable and one category of the second. In the cell it displays the count of rows that match that pair of categories.

For example, the table below shows that there were 28 men who were married and not working but looking for work. There were 171 men who were not married and were working as paid employees. And so on.

The pivot method takes as its first argument the name of the column that contains values to be used as column labels. Each unique value in this input column appears as a column in the contingency table. The second argument is the name of the column that contains values to be used as row labels. Each unique value in this input column appears in a separate row as the first entry. The third argument is the source of the values in the contingency table. In this case, counts are used and they are aggregated by summing.

Because the total number of married couples in the sample is greater than the number of unmarried couples, the counts in the different categories are not directly comparable. So we convert them into proportions, displayed in the last two columns of the table below. The married column shows the distribution of employment status of the married men in the sample. The partner column shows the distribution of the employment status of the unmarried men.

The two distributions look somewhat different from each other, as can be seen more clearly in the bar graphs below. It appears that a larger proportion of the married men work as paid employees, whereas a larger proportion of unmarried men are not working but are looking for work.

The difference in the two bar graphs raises the question of whether the differences are due to randomness in the sampling, or whether the distribution of employment status is indeed different for married men in the U.S. than it is for unmarried men who live with their partners. Remember that the data that we have are from a sample of just 1,034 couples; we do not know the distribution of employment status of men in the entire country.

We can answer the question by performing a statistical test of hypotheses. Let us use the terminolgoy that we developed for this in the previous section.

Null hypothesis. In the United States, the distribution of employment status among married men is the same as among unmarried men who live with their partners. The difference between the two samples is due to chance.

Alternative hypothesis. In the United States, the distributions of the employment status of the two groups of men are different.

As our test statistic, we will use the total variation distance between the two distributions. Because employment status is a categorical variable, there is no question of computing summary statistics such as means. By using the total variation distance, we can compare the entire distributions, not just summaries.

The observed value of the test statistic is about 0.15:

The Null Hypotheis and Random Permutations¶

The next step is important but subtle. In order to compare this observed value of the total variation distance with what is predicted by the null hypothesis, we need the probability distribution of the total variation distance under the null hypothesis. But the probability distribution of the total variation distance is quite daunting to derive by mathematics. So we will simulate numerous repetitions of the sampling procedure under the null hypothesis.

With just one sample at hand, and no further knowledge of the distribution of employment status among women in the U.S., how can we go about replicating the sampling procedure? The key is to note that if marital status and employment status were not connected in any way, then we could replicate the sampling process by replacing each oman's employment status by a randomly picked employment status from among all the men, married or unmarried. Doing this for all the men is equivalent to permuting the entire column containing employment status, while leaving the marital status column unchanged.

Thus, under the null hypothesis, we can replicate the sampling process by assigning to each married man an employment status chosen at random without replacement from the entries in empl_status. Since the first 742 rows of males correspond to the married men, we can do the replication by simply permuting the entire empl_status column and leaving everything else unchanged.

Let's implement this plan. First, we will shuffle the column empl_status using the sample method, which just shuffles all rows when provided with no arguments.

The first two columns of the table below are taken from the original sample. The third has been created by randomly permuting the original empl_status column.

Once again, the pivot method computes the contingency table, which allows us to calculate the total variation distance between the distributions of the two groups of men.

This total variation distance was computed based on the null hypothesis that the distributions of employment status for the two groups of men are the same. You can see that it is noticeably smaller than the observed value of the total variation distance (0.15) between the two groups in our original sample.

A Permutation Test¶

Could that just be due to chance variation? We will only know if we run many more replications, by randomly permuting the empl_status column repeatedly. This method of testing is known as a permutation test.

The figure above is the empirical distribution of the total variation distance between the distributions of the employment status of married and unmarried men, under the null hypothesis. The observed test statistic of 0.15 is quite far in the tail, and so the chance of observing such an extreme value under the null hypothesis is close to 0.

This chance is called a "P-value" in a hypothesis test. The P-value is the chance that our test statistic (TVD) would come out at least as extreme as the observed value (0.15 or greater) under the null hypothesis.

We can directly compute an empirical approximation to the P-value using the tvds we collected during the permutation test. The np.count_nonzero function takes a sequence of numbers and returns how many of them are not zero. When passed a list of True and False values, it returns the number that are True.

We call this p_value an empirical approximation because it is not the true chance of observing a TVD at least as large as 0.15. Instead, it is the particular result we happened to compute when shuffling randomly 200 times. Computing the true value would require us to consider all possible outcomes of shuffling (which is large) instead of just 200 random shuffles. Were we to consider all cases, there would be some with a more extreme TVD, and so the true P-value is greater than zero but not by much.

A low P-value constitutes evidence in favor of the alternative hypothesis. The data support the hypothesis that in the United States, the distribution of the employment status of married men is not the same as that of unmarried men who live with their partners.

In this example, our empirical estimate from sampling tells us all the information we need to draw conclusions from the data; the observed statistic is very unlikely under the null hypothesis. Precisely how unlikely often doesn't matter. Permutation tests of this form are indeed quite common in practice because they make few assumptions about the underlying population and are straightforward to perform and interpret.

Generalizing Our Hypothesis Test¶

The example above includes a substantial amount of code in order to investigate the relationship between two characteristics (marital status and employment status) for a particular subset of the surveyed population (males). Suppose we would like to investigate different characteristics or a different population. How can we reuse the code we have written so far in order to explore more relationships?

Functions allow us to generalize both the statistics we compute and the computational process of performing a permutation test. We can begin with a generalized computation of total variation distance between the distribution of any column of values (such as employment status) when separated into any two conditions (such as marital status) for a collection of data described by any table. Our implementation includes the same statements as we used above, but uses generic names that are specified by the final function call.

Next, we can write a function that performs a permutation test using this tvd function to compute the same statistic on shuffled variants of any table. It's worth reading through this implementation to understand its details.

Now that we have generalized our permutation test, we can apply it to other hypotheses. For example, we can compare the distribution over the employment status of women, grouping them by their marital status. In the case of men we found a difference, but what about with women? First, we can visualize the two distributions.

A glance at the two columns of proportions shows that the two distributions are different. The difference in the category "Not working – other" is particularly striking: about 22% of the married women are in this cateogory, compared to only about 8% of the unmarried women. There are several reasons for this difference. For example, the percent of homemakers is greater among married women than among unmarried women, possibly because married women are more likely to be "stay-at-home" mothers of young children. The difference could also be generational: as we saw earlier, the married couples are older than the unmarried partners, and older women are less likely to be in the workforce than younger women.

Let's review our reasoning about hypothesis testing. We have to consider the possibility that the difference could simply be the result of chance variation. Remember that our data are only from a random sample of couples. We do not have data for all the couples in the United States.

To test this, we set up null and alternative hypotheses. When setting up a hypothesis, the null in particular, it is important to be clear: exactly what are the unknowns about which you hypothesizing? In our example, the sample is entirely known, and the distributions of employment status in the two groups of women are simply different – the difference is visible in the data. The unknowns are the distributions of employment status among married and unmarried women in the United States, the population from which the sample was drawn. It is those distributions, in the population, about which we will form the competing hypotheses.

Null hypothesis: In the U.S., the distribution of employment status is the same for married women as for unmarried women living with their partners. The difference in the sample is due to chance.

Alternative hypothesis: In the U.S., the distributions of employment status among married and unmarried cohabitating women are different.

As with the males, the null hypothesis can be rejected because if it were true, something very unlikely occurred in this sample.

Age: A Quantitative Variable¶

Next, we can test the null hypothesis that the distributions in ages between married and cohabitating individuals are the same. Age is a quantitative variable — everyone has a different age. However, in our dataset, ages have been binned already into yearly categories.

It is perhaps no surprise that the empirical P-value is 0 (below); the idea that a couple would live together without being married has become more acceptable over time, and so we might expect that cohabitating couples are younger.

Looking at the distributions in ages confirms the result of this permutation test; the distributions simply look quite different. Here's a function that compares the distribution of values for two conditions. When called on 'mar_status' as the conditions, we compare the distributions of ages for mar_status=1 (married) and mar_status=2 (cohabitating).

What about the relationship of gender and age? Is there a difference in these distributions?

In this case, the women (gender=2) in the surveyed population of couples have an age distribution that skews a bit younger. Would this observed difference be a typical result of sampling if both the distributions of men and women in couples were in fact the same? According to our permutation_tvd test, the total variation distance between ages of these two groups is quite typical.

Further Generalization: New Test Statistics¶

Thus far, we have been looking at entire distributions, whether the variable is categorical, such as employment status, or quantitative, such as age. When we analyze quantitative variables, we can summarize the distributions by using measures such as the median and the average. These measures can be useful as test statistics – sometimes, working with them can be more efficient than working with the whole distribution. We will now generalize our methods of testing so that we can replace the total variation distance between distributions by other test statistics of our choice.

As part of the survey we have been studying, the sampled people were asked to rate their satisfaction with their spouse or partner. One of the questions they answered was, "Every relationship has its ups and downs. Taking all things together, how satisfied are you with your relationship with your spouse or partner?"

The question was in a multiple choice format, with the following possible answers:

• 1: very satisfied
• 2: somewhat satisfied
• 3: neither satisfied nor dissatisfied
• 4: somewhat dissatisfied
• 5: very dissatisfied

The answers given by the sampled people are in the column rel_rating of the table couples. More than 63% of the sampled people gave their satisfaction the highest possible rating:

Let us examine whether this rating is related to age. Perhaps older people are more appreciative of their relationships, or more frustrated; or perhaps high satisfaction with the spouse or partner has nothing to do with age. As a first step, here are the histograms of the ages of sampled people who gave the highest rating, and those who did not.

The two distributions are different, but they are also similar in many ways. This raises the question of how the two distributions compare in the U.S. population.

To answer this, we start by setting up null and alternative hypotheses.

Null hypothesis. Among married and cohabitating people in the United States, the distribution of ages of those who give the highest satisfaction rating is the same as the distribution of ages who do not. The difference in the sample is due to chance.

Alternative hypothesis. Among married and cohabitating people in the United States, the distribution of ages of those who give the highest satisfaction rating is different from the distribution of ages who do not.

Let us see if we can answer the question by just comparing the medians of the two distributions in the sample. As our test statistic, we will measure how far apart the two medians are.

Formally, the test statistic will be the absolute difference between the medians of the ages of the two groups.

The median age of those who gave the highest rating is one year more than the median of those who did not. The observed value of our test statistic is therefore 1.

To see how this statistic could vary under the null hypothesis, we will perform a permutation test. The test will involve repeatedly generating permuted samples of ages of the two groups, and calculating the test statistic for each of those samples. So it is useful to define a function that computes the test statistic – the absolute differeence between the medians – for every generated sample.

Like the function tvd, the function abs_diff_in_medians takes as its arguments the table of data, the name of a column of conditions that come in two categories, and the name of the column of values to be compared. It returns the absolute difference between the median values under the two conditions. By applying this function to the original sample, we can see that it returns the observed value of our test statistic.

To run the permutation test, we will define a function permutation_stat that is similar to permutation_ tvd except that it takes a fourth argument. This argument is the name of a function that computes the test statistic. The code is the same as for permutation_tvd apart from the number of repetitions and the replacement of tvd by the generic function stat.

Because permutation_test takes a function as an argument, it is called a higher order function.

Let us run the permutation test using abs_diff_in_medians to compute the test statistic. The empirical histogram of the test statistic shows that our observed value of 1 is typical under the null hypothesis.

The absolute difference between the medians does not reveal a difference between the two underlying distributions of age. As you can see from the empirical histogram above, the test statistic is rather coarse – it has a small number of likely values. This suggests that it might be more informative to compare means instead of medians.

The functions that we have developed make it easy for us to run the permutation test again, this time with a different test statistic.

The new test statistic is the absolute difference between the means.

As before, we will define a function that computes the test statistic based on a sample. Applying this function to the orignial sample shows that the observed means of the two groups differ by about 1.07 years.

The function permutation_stat performs the test, this time using abs_diff_in_means to compute the test statistic. The empirical P-value is in the 4% to 6% range. It is reasonable to conclude that the test gives no clear signal about whether the two underlying distributions are different; in such a situation, the conservative conclusion is that there is not enough justification to reject the null hypothesis in favor of the alternative.

What the test does reveal, however, is that the empirical distribution of the test statistic – the absolute difference between the two sample means – has a recognizable shape. It resembles one half of a bell. If you reflect the histogram about the vertical axis, the two pieces together will look like a bell.

To explore this observation further, we will run the permutation test again, this time using the difference between the means (without the absolute value) as our test statistic. To be consistent about the sign of the difference, we will compute the difference as "mean age of Group 1 - mean age of Group 2," where Group 1 comprises the people who give the highest rating and Group 2 the people who don't. The observed value of this new test statistic is still about 1.07 (the sign is positive), because Group 1 in the sample is on average older than Group 2.

The empirical distribution of the new test statistic looks like a bell. The surface of the bell is a bit rough, and the bell has a few dents here and there, but it is recognizably a bell.

The bell curve, formally known as the normal curve, is one of the fundamental distributions of probability theory and statistics. It arises principally in connection with probability distributions of the means of large random samples. We will discuss this more fully in later sections.

For now, observe that because the empirical distribution of the difference in means is roughly symmetric, the proportion to the right of 1.07 is about the same as the proportion to the left of -1.07. Therefore, multiplying the P-value by 2 gives an answer that is very close to the P-value of the previous test – the one that used the absolute difference in means as its test statistic. Indeed, if you fold the bell about the vertical axis and stack each bar above its reflection, you will get a histogram that looks very much like the tall "half bell" of the previous test.

One-tailed and two-tailed tests.

In classical statistics, tests of hypotheses using sample means typically involve calculating P-values using the bell shaped curve rather than the "folded over" version. If you read a classical analysis, you might see the term "one-tailed test" used to describe the situation in which the P-value is computed as the proportion in one tail of the bell. A "two-tailed test" uses the total proportion in two equal tails, and is thus equivalent to the test we conducted using the folded-over bell.

But as you have seen, in practical terms the tests are essentially equivalent. If you know the P-value of one, you can calculate the P-value of the other. Just be aware that sometimes, as in our examples above, the one-tailed test might give a statistically significant result while the two-tailed test does not. Such results are not contradictory – they merely point out a difficulty in rigid adherence to a fixed cutoff determining "small" values of P.

The Probability Distribution of a Sample Mean¶

Means of large random samples have a wonderful property that is at the heart of much statistical inference: their probability distributions are roughly bell shaped. This property allows us to determine how variable a random sample mean could be, based on just one sample, without any simulation at all.

To see why this is important, consider the basis on which we have been conducting our simulations of repeated sampling.

For repeated sampling to be feasible, we need to know what to resample from. The null hypothesis specifies the chance model. In the jury panel examples, the populations of eligible jurors were known, and the null hypothesis said that the panels were drawn at random. So we simulated random sampling from the known distributions of eligible jurors. In the case of marital status and employment status, the null hypothesis allowed us to compare married and unmarried people by randomizing them into the different employment categories.

But what if the situation does not allow either of these two options? For example, suppose we have just one random sample of California households this year, and are trying to see whether the average annual household income in California exceeds $61,000, which was roughly the average annual income in California last year. How can we replicate the sampling procedure? The underlying distribution of the population is unknown (indeed, its mean is what we're trying to get at), and there is no other sample to which we can compare ours.

One way to solve this problem is to avoid replication entirely, and use other methods to approximate the probability distribution of the test statistic. If the test statistic is a sample mean, the theory of probability and statistics tells us that its probability distribution will be roughly bell shaped if the sample is large, no matter what the distribution of the underlying population looks like. This powerful result not only allows us to make inferences when replication is not straightforward, it also illuminates some important general properties of large random samples.

This chapter will help us understand all of this better. We will start by examining some fundamental properties of means.

Properties of the mean¶

Definition: The average or mean of a list of numbers is the sum of all the numbers in the list, divided by the number of entries in the list.

In this course, we will use the words "average" and "mean" interchangeably.

Computation: We have computed means in two different ways. One is the Table method mean(), and the other is the numPy function np.mean. Here we use these two ways to calculate the average age of the people in our random sample of couples.

We can, of course, just compute the mean by directly applying its definition. Let's do this for a list x_list consisting of 15 elements.

The calculation shows that the average of x_list is $3 \frac{1}{3}$. But it also makes us wonder whether the calculation can be simplified by using the fact that there are only four distinct values in the list: 4, 5, 2, and 3. When we add up all the entries to get the numerator of the average, we can collect all the terms correpsonding to each distinct value, and save ourselves some addition:

Distributing the division by 15 across all the terms in the numerator shows that we can calculate the average in terms of the distinct values and the proportions in which they appear:

The Average and the Histogram¶

We have just seen that the average of a list depends only on the distinct values and their proportions. In other words, the average is a property of the distribution of distinct values in the list.

Here is x_list represented as a distribution table x_dist. The average can be calculated by multiplying the value column by prop and then adding the results.

Another way to think about the mean. The mean of a list is the weighted average of the distinct values, where the weights are the proportions in which those values appear.

Physically, this implies that the average is the balance point of the histogram. Here is the histogram of the distribution. Imagine that it is made out of cardboard and that you are trying to balance the cardboard figure at a point on the horizontal axis. The average of $3 \frac{1}{3}$ is where the figure will balance.

To understand why that is, you will have to study some physics. Balance points, or centers of gravity, can be calculated in exactly the way we calculated the mean from the distribution table.

Summary of Basic Properties of the Mean¶

These properties follow from the calculation; we have observed most of them in our examples above.

• The mean has the same units as the list.
• The mean is somewhere in between the smallest and largest value on the list.
• The mean depends only on the distribution (distinct values and proportions), not on the number of entries in the list.
• The mean is the balance point of the histogram.

The Average and the Median¶

Now that we know that the mean is the balance point of the histogram, it is interesting to look at how it is related to the median, which is the "half-way point" of the sorted data.

In terms of the histogram, we would like to compare the balance point to the point that has 50% of the area of the histogram on either side of it.

The relationship is easy to see in a simple example. Here is the list 1, 2, 2, 3, represented as a distribution table sym for "symmetric".

The histogram (or a calculation) shows that the average and median are both 2.

In general, for symmetric distributions, the mean and the median are equal.

What if the distribution is not symmetric? We will explore this by making a change in the histogram above: we will take the bar at the value 3 and slide it over to the value 10.

The yellow histogram represents the original distribution; the blue histogram starts out the same as the yellow at the left end, but its rightmost bar has slid over to the value 10.

The median and mean of the yellow distribution are both equal to 2. The median of the blue distribution is also equal to 2; the area on either side of 2 is still 50%, though the right half is distributed differently from the left.

But the mean of the blue distribution is not 2: the blue histogram would not balance at 2. The balance point has shifted to the right:

In general, if the histogram has a tail on one side (the formal term is "skewed"), then the mean is pulled away from the median in the direction of the tail.

We have seen an example of a distribution with a right-hand tail: the box office gross receipts (in millions of dollars) of the highest grossing movies over the past couple of decades:

The mean gets pulled away from the median in the direction of the tail. So we expect the mean to be larger than the median, and that is indeed the case:

Another example. Distributions of incomes often have right hand tails. For example, most households in the United States have low to moderate annual incomes, and a small number have extremely large annual incomes by comparison. In other words, the distribution of annual household incomes in the United States has a long right hand tail. So the mean income is greater than the median; the mean is affected by the small number of very large incomes, whereas the median is not. That is why the median is used more frequently than the mean in summaries of income distributions.

The Rough Size of Deviations from Average¶

As we have seen, inferences based on test statistics depend on how those statistics vary across samples. It is therefore important to be able to quantify the variability in any list of numbers. One way is to create a measure of the difference between the values on a list and the average of the list.

We will start by defining such a measure in the context of a simple list of just four numbers.

The goal is to get a measure of roughly how far off the numbers in the list are from the average. To do this, we need the average, and all the deviations from the average. A "deviation from average" is just a value minus the average.

Some of the deviations are negative; those correspond to values that are below average. Positive deviations correspond to above-average values.

To calculate roughly how big the deviations are, it is natural to compute the mean of the deviations. But something interesting happens when all the deviations are added together:

The positive deviations exactly cancel out the negative ones. This is true of all lists of numbers: the sum of the deviations from average is zero. We saw this kind of property earlier, when we were defining total variation distance.

Since the sum of the deviations is 0, the mean of the deviations will be 0 as well:

So the mean of the deviations is not a useful measure of the size of the deviations. What we want to know is roughly how big the deviations are, regardless of whether they are positive or negative. So we eliminate the signs by squaring all the deviations; then we take the mean of the squares:

The mean squared deviation is called the variance of the list. While it does give us an idea of spread, it is not on the same scale as the original variable and its units are the square of the original. This makes interpretation very difficult. So we return to the original scale by taking the positive square root of the variance:

Standard Deviation¶

The quantity that we have just computed is called the standard deviation of the list, and is abbreviated as SD. It measures roughly how far the numbers on the list are from their average.

Definition. The SD of a list is defined as the root mean square of deviations from average. That's a mouthful. But read it from right to left and you have the sequence of steps in the calculation.

Computation. The numPy function np.std computes the SD of values in an array:

Why use the SD instead of some other measure of spread? Answer #1.¶

There are a few primary reasons the SD is used more than any other measure of spread. Here is one of them.

If you know the average of a list, typically you can't infer much else about the spread in the list. You can't even infer that half the list is above average, because, as we have seen, the average and the median are typically different from each other.

If you know both the average and the SD, however, you can learn a great deal about the values in the list.

Informal statement.

For all lists, the bulk of the entries are within the range "average $\pm$ a few SDs".

Try to resist the desire to know exactly what fuzzy words like "bulk" and "few" mean. We wil make them precise later in this section. For now, let us examine the statement in the context of the example of box office receipts.

The mean is \$174.29, and the SD is \$86.15. Notice that none of the entries on the list are below the amount "mean - SD". Indeed, none are below \$100 million. The large spread is due to the large positive deviations in the right hand tail.

In the analysis of distributions, specially those that have been represented in a histogram, it is often useful to think of the average as the origin, and distances in units of SDs. For example, here is the interval "mean $\pm$ one SD"; about 87.5% of the movies have box office receipts in this range.

The table below contains intervals of the form "mean $\pm$ a few SD", and the proportions of entries in that range. The column z quantifies the expression "a few". As you can see, once z is about 4 or so, the interval "average $\pm z$ SD" contains almost all of the data.

This kind of behavior is true of all lists, not just the ones in our examples.

Chebychev's inequality¶

This is the formal version of our rough statement above:

For all lists, and all positive numbers z, the proportion of entries that are in the range "average $\pm z$ SDs" is at least $1 - \frac{1}{z^2}$.

What makes this result powerful is that it is true for all lists – all distributions, no matter how irregular, known or unknown. Specifically, Chebychev's inequality says that for every list:

• the proportion in the range "average $\pm$ 2 SDs" is at least 1 - 1/4 = 0.75

• the proportion in the range "average $\pm$ 3 SDs" is at least 1 - 1/9 $\approx$ 0.89

• the proportion in the range "average $\pm$ 4.5 SDs" is at least 1 - 1/$4.5^2$ $\approx$ 0.95

Chebychev's Inequality gives a lower bound, not an exact answer or an approximation. The proportion of entries in the range "average $\pm z$ SDs" might be quite a bit larger than $1 - 1/z^2$. But it cannot be smaller.

Interpreting $z$

$z$ is the number of SDs above average, and is said to be on the standard units scale.

Some values of standard units are negative, corresponding to original values that are below average. Other values of standard units are positive. But no matter what the distribution of the list looks like, Chebychev's Inequality says that standard units will typically be in the (-5, 5) range.

Here are some examples of moving back and forth between the original scale and the standard units scale. Recall that the average box office amounts of our list of movies is $m = \$174.29$ and the SD is $s = \$86.15$.

Examples of converting from standard units to the original units. The calculation is straightforward if you remember that $z$ answers the question, "How many SDs above average is the original value?"

If $z = 2.4$, then the movie made $z*s + m = 2.4*86.15 + 174.29 = 381.05$ million dollars.

If $z = -0.3$, then the movie made $z*s + m = (-0.3)*86.15 + 174.29 = 148.45$ million dollars.

Examples of converting from the original units to standard units. First find how far above average the value is on the original scale, then compare the difference with the SD.

If the movie made 220 million dollars, then $z = (220 - 174.29)/86.15 = 0.53$.

If the movie made 120 million dollars, then $z = (120 - 174.29)/86.15 = -0.63$.

In probability and statistics, $z$ is standard notation for values on the standard units scale. Converting to standard units is also known as "finding the $z$-score".

If we know more about the shape of a distribution than just its average and SD, we might have additional tools to work with it. This section investigates one famous shape of a distribution: the bell curve of the normal distribution.

The Normal Distribution¶

Some probability histograms are roughly bell shaped, as we have seen. Some distributions of data are also bell shaped, to a rough approximation. For example, here is a histogram of the heights of over 1,000 women. As you can see, it is roughly bell shaped.

The heights of the women have an average of just about 64 inches, and an SD of just about 2.5 inches. The range "average $\pm$ 2 SDs" is roughly 59 inches to 69 inches. Chebychev's inequality says that this range should contain at least 75% of the data, regardless of the shape of the distribution. For this histogram, the interval 59 inches to 69 inches contains quite a bit more than 75% of the data.

Is it possible to say something more precise than "quite a bit more," by examining the bell more closely? Let us explore this question, by studying a smooth curve that looks like a bell.

The standard normal curve¶

The bell shaped curve of probability and statistics has an impressive equation. But for now, it is best to think of it as a smoothed version of a histogram of a variable that has been measured in standard units.

$$ \phi(z) = {\frac{1}{\sqrt{2 \pi}}} e^{-\frac{1}{2}z^2}, ~~ -\infty < z < \infty $$

In order to work with and display this equation, we need to import some additiona modules.

As always when you examine a new histogram, start by looking at the horizontal axis. On the horizontal axis of the standard normal curve, the values are standard units. Here are some properties of the curve; some are apparent by observation, and others require a considerable amount of mathematics to establish.

• The total area under the curve is 1. So you can think of it as a histogram drawn to the density scale.

• The curve is symmetric about 0. So if a variable has this distribution, its mean and median are both 0.

• The points of inflection of the curve are at -1 and +1.

• If a variable has this distribution, its SD is 1. The normal curve is one of the very few distributions that has an SD so clearly identifiable on the histogram.

Since we are thinking of the curve as a smoothed histogram, we will want to represent proportions of the total amount of data by areas under the curve. Areas under smooth curves are often found by calculus, using a method called integration. It is a remarkable fact of mathematics, however, that the standard normal curve cannot be integrated in any of the usual ways of calculus. Therefore, areas under the curve have to be approximated. That is why almost all statistics textbooks carry tables of areas under the normal curve; it is also why all statistical systems, including the stats module of Python, include methods that provide excellent approximations to those areas.

The standard normal cumulative distribution function (cdf)

The fundamental function for finding areas under the normal curve is stats.norm.cdf. It takes a numerical argument and finds all the area under the curve to the left of that number. Formally, it is called the "cumulative distribution function" of the standard normal curve. That rather unwieldy mouthful is abbreviated as cdf.

Let us use this function to find the area to the left of $z=1$ under the standard normal curve.

That's about 84%. We can apply the function stats.norm.cdf to find other areas under the curve too. For example, suppose we want to find the area between $-1$ and 1:

We can start with the area to the left of 1:

and subtract from it the area to the left of $-1$:

Here is the calculation using stats.norm.cdf.

We can use the symmetry of the curve to check that this answer makes sense. The area to the left of 1 is about 84%, as we saw earlier. Since the total area under the curve is 1 or 100%, the unshaded area in the graph above is about 16%. Since the curve is symmetric, the blue area is about 16% too. So the total area in the two tails is about 32%, and the yellow central area is therefore just about 68%.

By a similar calculation, we see that the area between $-2$ and 2 is about 95%.

In other words, if a histogram is roughly bell shaped, the proportion of data in the range "average $\pm$ 2 SDs" is about 95%. That is indeed "quite a bit more" than Chebychev's lower bound of 75%, as we had observed earlier.

Percentiles of the standard normal curve

We say that the value $z=1$ roughly the 84th percentile of the standard normal curve, since 84% of the area under the curve is to the left of 1. The informal terminology is that the point $z=1$ is roughly the 84 percent point of the curve.

Percentiles, or percent points, can be found using the stats.norm.ppf function, which takes a proportion as its argument, and returns the point that has that proportion of the area to the left of it.

This is just about 1, as we expect. Notice that percentiles below 50% correspond to negative values of $z$. The 40th percentile of the distribution is approximately $z = -0.25$.

The normal approximation to data

There are many normal curves, one corresponding to each pair of mean and SD. Their horizontal axes can all be converted to standard units, turning them all into the standard normal curve that we have been studying. But we can study them directly too.

Example 1. A distribution of weights follows the normal curve very closely, with mean 160 pounds and SD 20 pounds. Approximately what is the 75th percenile of the weights?

From our earlier observations, 160 pounds is the 50th percentile of the weights, and 180 pounds is roughly the 84th. So the 75th must be somewhere in the interval 160 pounds to 180 pounds. We can find it by calling stats.norm.ppf and including the mean and SD as its second and third argument respectively:

Approximately 75% of the weights are less than 173.49. This is consistent with the graph below.

It is worth noting that this problem can also be solved by finding the answer in standard units first, and then converting the standard units into pounds. When stats.norm.ppf is called without a mean or an SD as arguments, the default is that the curve is in standard units.

Example 2.

About what percent of the weights are more than 130 pounds?

To answer this, we can use stats.norm.cdf by including the mean and SD as arguments, and recalling that it finds all the area to the left of its first argument.

This problem can also be solved by first converting 130 pounds to standard units and then calling stats.norm.cdf with its default curve, the standard normal:

When working with the normal curve, it is a good idea to make rough sketches and shade the relevant areas. That makes it easier to see what has to be calculated, and also to see whether the answers make sense.

Approximately Normal Probability Histograms¶

We have noticed earlier that the empirical distributions of some statistics turn out roughly bell shaped. Now that we know how to work with the bell shaped curve, we can better understand which distributions turn out to be bell shaped, and exactly which bells they resemble.

We will start by revisiting the data on the highest grossing movies of the past couple of decades. There are over 600 movies on our list. The histogram below shows their box office gross amounts in millions of dollars.

By the law of averages, the empirical histogram of a large random sample from this population should resemble the histogram of the population. This is demonstrated in the histogram of a random sample of size 400 taken with replacement:

So it is reasonable to expect that if we use the mean of the sample as an estimate of the mean of the population, we will not be very far off. The mean of the population is about 174.29 million dollars:

And the mean of the sample is about 177 million dollars:

Could another sample have had a mean further away from the population mean? To answer this, we will use one of the main methods of this course: simulate! The function samp_means takes a sample size n as its argument, and performs 4000 replications of the following simulation:

• Draw n times at random with replacement from the list of box office receipts, and compute the mean of the sample.

Once it has computed all 4000 sample means, it draws their histogram and provides some summary statistics.

Let us call samp_means with sample sizes of 25, 100, and 400.

All three histograms balance very close to 174.29, the population mean. The bigger the sample size, the closer the balance point is to the population mean. This leads to a restatement of the Law of Averages, this time in terms of sample averages instead of sample proportions.

Law of Averages, restated¶

As the sample size gets larger, the average of a random sample tends to get closer to the average of the population.

But we have observed something more: the shapes of all the histograms look like bells. Putting this together with our observation about the average gets us close to one of the greatest theorems in all of probability and statistics:

The Central Limit Theorem (first attempt)¶

When the sample size is large, the probability distribution of the average of a random sample (drawn with replacement) is approximately bell shaped, with

• mean equal to the mean of the population, and
• SD equal to ...

Well, we don't quite know the SD yet, but we can see that it is getting smaller as the sample size increases. In other words, as the sample size increases, the sample mean is more likely to be close to the population mean. But how close?

The variability in the sample average¶

Let us take a look at the SDs in the graphs above. In all three of them, the SD of the population is about 86 million dollars; all the samples were taken from the same population. Now look at the SD of empirical histogram of the sample mean, when the sample size is 100. That SD is about one-tenth of the population SD. When the sample size is 400, the SD of the sample means is about one-twentieth of the population SD. When the sample size is 25, the SD of the sample means is about one-fifth of the population SD.

It seems like a good idea to compare the SD of the emirical distribution of the sample means to the number "population SD divided by the square root of the sample size."

Here are the numerical values. For each sample size in the first column, 4000 sample means were simulated; the second column contains the SD of those 4000 means. The third column contains the result of the calculation "population SD divided by the square root of the sample size."

If we plot the second and third columns with the first column on the horizontal axis, the two graphs are essentially indistinguishable:

Remember that the graph above is based on 4000 replications for each sample size. But there are many more than 4000 samples of sizes 25 or more.

The probability distribution of the sample mean is based on the means of all possible samples of a fixed size.

The SD of all these possible sample averages has a special name.

$$ {\bf\mbox{Standard Error (SE) of the sample average}} ~=~ \frac{\mbox{Population SD}}{\sqrt{\mbox{sample size}}} $$

This is the standard deviation of the list of averages of all possible samples that could be drawn.

The SE of the sample average measures roughly how far off the sample average is from the population average.

We now have a very good idea about the SD in the Central Limit Theorem. It is not just decreasing: we know that it is decreasing according to a function that we have identified.

The Central Limit Theorem (second attempt)¶

When the sample size is large, the probability distribution of the average of a random sample (drawn with replacement) is approximately bell shaped, with

• mean equal to the mean of the population, and
• SD equal to the SE of the sample average: $\frac{\mbox{Population SD}}{\sqrt{\mbox{sample size}}}$

At this stage it is worth pausing to consider whether this remarkable regularity of the behavior of random sample means might somehow be related to the population from which we are drawing the samples, namely, the population of box office gross receipts.

Let us carry out the steps above using a different population. The new population consists of one value for each zipcode in California: the value is the number of household tax returns filed in that zipcode in 2013. The returns are measured in thousands. Here is a histogram of the population.